Dijkstra's algorithm

다익스트라 알고리즘은 하나의 정점 에서 다른 모든 정점으로 가는 최단 경로 탐색 알고리즘이다.
알고리즘에 대한 자세한 설명은 건너뛰고 구현위주로 작성하겠다.

• 벡터
• 배열
• 우선순위 큐

C++로 다익스트라 구현하기 위해 위 3가지가 필요하다.

우선 정점의 개수가 N개라고 가정을 하자.

벡터는 다음과 같이 선언할 것이다. (1번 정점부터 N번 정점까지 저장해야하기에 N+1)

vector<pair<int, int>> vertex[N+1];

vertex[i] : i번 정점
vertex[i]의 원소 :pair( i에서 갈 수 있는 다른 정점 , 그 정점까지의 가중치 )

예를 들어 다음 그래프에서 vertex[1]과 vertex[2]의 원소는 다음과 같다.

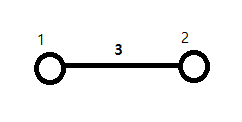
방향성이 없는 그래프이므로 서로에 대한 정보를 가진다.
vertex[1][0] = (2,3)
vertex[2][0] = (1,3)

다음으로 선언해줄 것은 최단거리를 저장할 배열이다.

INF(무한)로 초기화를 해준다.

int D[N+1];
for(int i=1;i<=N;i++)D[i]=INF;

마지막으로 우선순위 큐 priority_queue가 필요하다.(#include <queue>)

우선순위 큐는 큐와 다르게 원소 중 값이 가장 큰 값을 가장 먼저 빼준다.
다익스트라에서는 값이 가장 작은 순으로 꺼내야하기에 거리에 -를 해주어 큐에 넣을 것이다.

priority_queue<pair<int, int>> PQ;

이제 구현해보자.

시작 정점 v1을 인자로 넣어주면 v1에서 다른 모든 정점으로의 최단 거리를 배열에 저장해 주는 함수를 구현할 것이다.

//#include <bits/stdc++.h>
#include <vector>
#include <queue>
#define INF 2'100'000'000
vector<pair<int, int>> vertex[N+1];
int D[N+1]; //배열은 INF로 초기화된 상태

void dijkstra(int v1)
{
    priority_queue<pair<int, int>> PQ;

    //시작정점 v1에서 v1까지의 거리는 0이므로
    PQ.push(make_pair(0,v1));
    D[v1]=0;

    //큐가 비어질 때까지 반복한다.
    while(!PQ.empty())
    {
        //v1에서 지금 보고있는 정점까지의 비용
        int Cost = -PQ.top().first;

        //지금 보고있는 정점
        int Ver = PQ.top().second;
        PQ.pop();

        //큐에서 꺼낸, 지금 보고있는 정점까지의 거리가 현재 저장된 최단거리보다 큰경우
        //꺼낸 거리에서 다른 정점으로 가는 건 최단거리가 아니기에 패스한다.
        if(Cost>D[Ver]) continue;

        //지금 보고있는 정점에서 갈 수 있는 다른 모든 정점까지의 거리를 보기위해 반복
        for(int i=0;i<vertex[Ver].size();i++)
        {
            //Ver에서 갈 수 있는 정점
            int nextVer = vertex[Ver][i].first;

            //Ver에서 nextVer까지의 거리
            int nextCost = vertex[Ver][i].second;

            //Ver에서 nextVer로 가는 거리가 현재 저장된 최단거리보다 작으면
            if(D[Ver]+nextCost < D[nextVer])
            {
                //최단경로를 갱신해준다.
                D[nextVer] = D[Ver]+nextCost;

                //갱신되었으므로 우선순위 큐에 넣어줌
                PQ.push(-D[nextVer], nextVer);
            }
        }
    }
}

위 함수가 실행되면 D[i]에는 v1에서 i까지의 최단거리가 저장되고 경로가 없는 경우 INF가 그대로 유지된다.

각 정점까지의 경로를 알고싶다면?

정점개수크기의 배열 int path[N+1]을 선언해주고 최단경로가 갱신될 때마다 path[nextVer]에 Ver를 저장해주면 된다.

함수가 끝난 뒤, path[i]에는 i까지 최단거리로 이동할 때 i이전의 정점이 저장되기에 추적해주면 된다.

방향성이 있는 그래프에서 모든 정점에서 K번 정점까지의 거리를 알고싶다면?

모든 정점에서 각각 다익스트라를 돌려서 즉, N번 돌려서 구할 수 있다.

하지만 한번으로 구하는 것이 가능하다.

그래프의 방향을 반전시켜 K에서 다익스트라를 구하면 된다!!